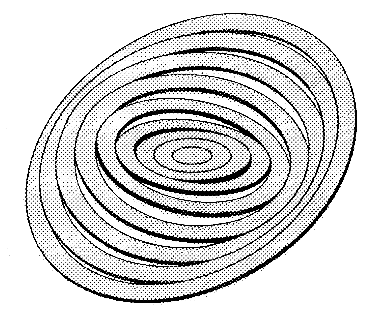
Tilted Ring Fitting Code

	Tilted-ring model of M83 by Rogstad et al. (1974)
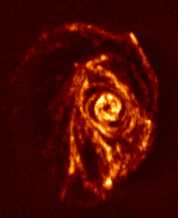	The H i distribution of M83 as observed more recently with the Parkes telescope and the ATCA (image made by Park et al.). Note that Rogstad et al. saw only a small portion of the H i distribution shown here.

Tilted Ring Fitting Code (TiRiFiC) is a computer program to construct simulated (high-resolution) astronomical spectroscopic 3d-observations (data cubes) of simple kinematical- and morphological models of rotating (galactic) disks. It is possible to automatically optimise the parametrisations of constructed model disks to fit spectroscopic (3d-) observations via a χ² minimisation. TiRiFiC depends on several free non-standard libraries, but is a standalone routine (after compilation). In former development stages, TiRiFiC has been implemented as a task in the Groningen Image Processing System (GIPSY) software package. From version 2.2.0 on, the GIPSY implementation is not longer supported and will not be installed. The source code of TiRiFiC can be downloaded from this web page.

As such, we do not provide much information for the interested but unexperienced layman (although you are of course invited to browse through our pages). However, we will try to add a generally understandable introduction. Alas, this will probably not happen until a far future.

A very brief introduction

The tilted-ring model is a very successful approach to describe the kinematics (and the morphology) of rotating disks (e.g. spiral galaxies) as observed in spectral line experiments. Various software packages exist that anable the user to automatically fit a tilted-ring models to (wide-field) spectroscopic observations of a tracer material in rotating disks. One class, fit algorithms to velocity fields, has its shortcomings in the systematic bias introduced by beam smearing and a limitation to certain gometric properties of the investigated targets. The second class, direct fitting routines to data cubes, while applicable to much more general cases, is usually too slow to be useful and the implementation too simplistic.

The TiRiFiC goals are:

• to extend the tilted-ring model enabling the user to account for inhomogeneities in galaxy disks, to make it suitable for deep surveys (like HALOGAS).
• to provide a tool to automatise galaxy parametrisations in large spectroscopic surveys (like WNSHS with Apertif at the WSRT and WALLABY with the ASKAP).

The code and its description are available on these www pages. We cordially invite you to provide feedback and suggestions.

For a detailed description, please follow the links on the left (or here):

A brief introduction

The tilted-ring model has been introduced by Rogstad et al. (1974) as a possibility to describe the neutral gaseous disk of the galaxy Messier 83. Simulating the observed H i (neutral-Hydrogen) distribution of the galaxy as a set of circular, concentric, but mutually inclined, rotating rings, they were able to show that M83 most likely has a warped disk (although people were not ready to believe yet; the undisputed, or only slightly disputed, proof of the existence warps in the outer H i layers of spiral galaxies was provided later by Sancisi (1976)). Today we know that most galactic disks exhibit warps once the restoring gravitational forces of the inner disk become weak at large radii, which is why the tilted-ring model has become the favourite kinematical model for galactic H i disks (since H i usually extend far beyond the massive inner stellar disk). Also TiRiFiC (after nearly 40 years) is a software to describe a galaxy within that framework.

There are basically two classes of techniques to construct a tilted-ring model from a given intensity distribution (the intensity I(ξ, η, λ) = I(ξ, η, ν(λ)) is the brightness of a source in dependence of the position on the sky (ξ, η) and the frequency ν or the wavelength λ and with that, via the Doppler shift, of the recession velocity V(ν): I(ξ, η, ν)= I(ξ, η, V(ν)) ; the representation of the observed intensity projected onto a 3d-grid, i.e. the result of a wide-field spectroscopic observation, is called a "data cube").

Fitting to velocity fields

One class works by first constructing a so-called velocity field, a map representing the mid-plane recession velocity of the disk, to then fit a tilted-ring model to this kinematical map. This technique has been explored in detail and expanded by Begemann (1987) (rotcur, implemented in GIPSY), Schoenmakers (1999) (reswri, implemented in GIPSY), Spekkens & Sellwood (2007) (diskfit), Krajnovic (2006) (KINEMETRY) and others. The advantages of this method are (for a detailed discussion see e.g. Józsa et al. 2007):

• Speed: velocity field methods tend to be fast and were hence suitable for automated fitting processes even in the past (e.g. 1987).
• Beam smearing: due to the coupling of data points in a velocity map (beam smearing), parametrisations are smoothed out. Beam smearing hence provides an inherent regularisation scheme
• Insensitivity to surface-brightness variations: The distribution of material in observed objects is usually not rotationally symmetric (see image of M83). By only taking into account the velocity in fitting processes, one avoids the necessity to take these inhomogeneities into account (rotational asymmetries in velocity stay an issue)

The disadvantages of this method are (for a detailed discussion see e.g. Józsa et al. 2007):

• Beam smearing: due to the coupling of data points in a velocity map (beam smearing), parametrisations are systematically biased.
• Limited model: key parameters such as surface brightness and disk thickness cannot be directly accessed (there are ways to recover at least the surface brightness profile, though).
• Ambiguity: it is not possible to construct a velocity field in all cases. E.g. for edge-on disks (disks with usually an inclination above 75°) a velocity field cannot be constructed.

Fitting to data cubes

The other class of tilted-ring parametrisation techniques consists of constructing parametrised model datacubes, simulating observations, which are then compared directly to the observations. The most commonly used routine of that group so far is the GIPSY routine galmod in combination with a convolution task. galmod has no optimisation loop, such that models are fitted "by eye". Extensions of galmod have been used to account for the vertical (kinematical) fine structure of galaxies (Fraternali et al. 2002, Heald et al. 2006). An automated optimisation of parametrised data cubes has been implemented by Corbelli & Schneider (1997) and later by Fiege et al. (GalAPAGOS) and Józsa et al. (2007) (TiRiFiC, this web page). The advantages of this method are (for a detailed discussion see e.g. Józsa et al. 2007):

• No beam smearing: since an additional data reduction (and compression) step (construction of the velocity field) is left out, this is a direct comparison of the model to the data.
• Larger set of key parameters: a parametrisations connected to the observed intensity distribution (e.g. surface brightness profile) is part of the model. In principle any geometrical model can be fitted to the data.
• No geometrical limitations: the orientation of the observed disk plays a role only in the statistical uncertainties of the parametrisation.
• Fewer ambiguities: with the larger number of data points available for the comparison of model and observation, the level of ambiguity of parametrisations is reduced.

The disadvantages of this method are (for a detailed discussion see e.g. Józsa et al. 2007):

• Slowness: instead of a velocity field, a complete model data cube has to be constructed before it can be compared to the original observation. As a consequence, the first successful attempt of an automated direct fit to a data cube (which requires the computation of many models) was performed as late as 1997 (Corbelli & Schneider 1997). Before, this had been computationally too expensive, and the usual technique had been to make use of the GIPSY routine galmod to achieve a comparison "by eye".
• No beam smearing: with a direct comparison to the data, any regularisation of parametrisations has to be added artificially. This affects automated fitting routines.
• Larger set of key parameters: The necessity to expand the model increases the number of parameters that have to be fitted. Connected to that is a higher degree of possible ambiguity.
• Sensitivity to inhomogeneities: fitting to the data cube requires a prediction of the surface brightness distribution, which, in reality, is not homogeneous. The attempt to fit inhomogeneities may lead to inappropriate parametrisations (which is, however, also an issue when constructing velocity fields).

The purpose of TiRiFiC

TiRiFiC is an attempt to provide a method to automatically fit an extended tilted-ring model directly to a data cube. The goals are to overcome the drawbacks of fitting methods using velocity fields and to ultimately provide a tool to automatise galaxy parametrisations in large spectroscopic surveys. Both WNSHS with Apertif at the WSRT and WALLABY with the ASKAP) are projects, we are heavily involved with. But it is also our aim to provide a useful tool for the everyday use of the common (H i-) astronomer. As outlinedlined above, for a direct-fit method it is necessary:

• to optimise the computing speed.
• to extend the tilted-ring model enabling the user to account for inhomogeneities in galaxy disks.
• to find the means to provide smooth parametrisations

Especially the first two points have been addressed to some extent, while the third point is currently being investigated in an experimental phase (you are invited to take part). In this context, again, we cordially invite you to provide feedback and suggestions.

For a detailed description, please follow the links on the left (or here):